Notice
Recent Posts
Recent Comments
Link
250x250
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
Tags
- 묵상
- 날마다 솟는 샘물
- 설교
- 찬양
- 예배
- SQLD
- dbms
- Software Engineering
- Database
- 데이터베이스
- FE
- SQL
- 글로벌리더십학부
- CHEMISTRY
- 혼자공부하는sql
- 유태준교수님
- CCM
- csee
- GLS
- 웹개발
- 날솟샘
- typeScript
- 화학
- 한동대학교
- QT
- 프론트엔드
- 일반화학
- 전산전자공학부
- 어노인팅
- 남재창교수님
Archives
- Today
- Total
멈추지 않는 기록
[일반 화학] Chapter 5 - (2) 본문
728x90
5.5. 기체 화학량론
[1] 기체 화학량론

1) 기체 화학량론이란?
: 기체 화학량론은 기체 반응에서 물질의 양을 계산하는 방법이다.
- 총 4단계 : 반응물의 양 (그램 또는 부피) -> 반응물의 몰 -> 제품의 몰 -> 생성물의 양 (그램 또는 부피)
2) 단계 별 내용
- 반응물의 양 측정: 반응물의 질량(그램)이나 부피(리터)를 측정한다.
- 몰로 변환: 측정한 반응물의 양을 몰로 변환한다. (몰 수 = 질량(g) / 분자량(g/mol))
- 제품의 몰 계산: 반응식에 따라 반응물의 몰 수를 이용해 생성될 제품의 몰 수를 계산한다.
- 생성물의 양 계산: 마지막으로 계산한 제품의 몰 수를 질량(그램) 또는 부피(리터)로 변환하여 생성물의 양을 구한다.
5.6 달튼의 부분 압력의 법칙
[1] 달튼의 부분 압력 법칙
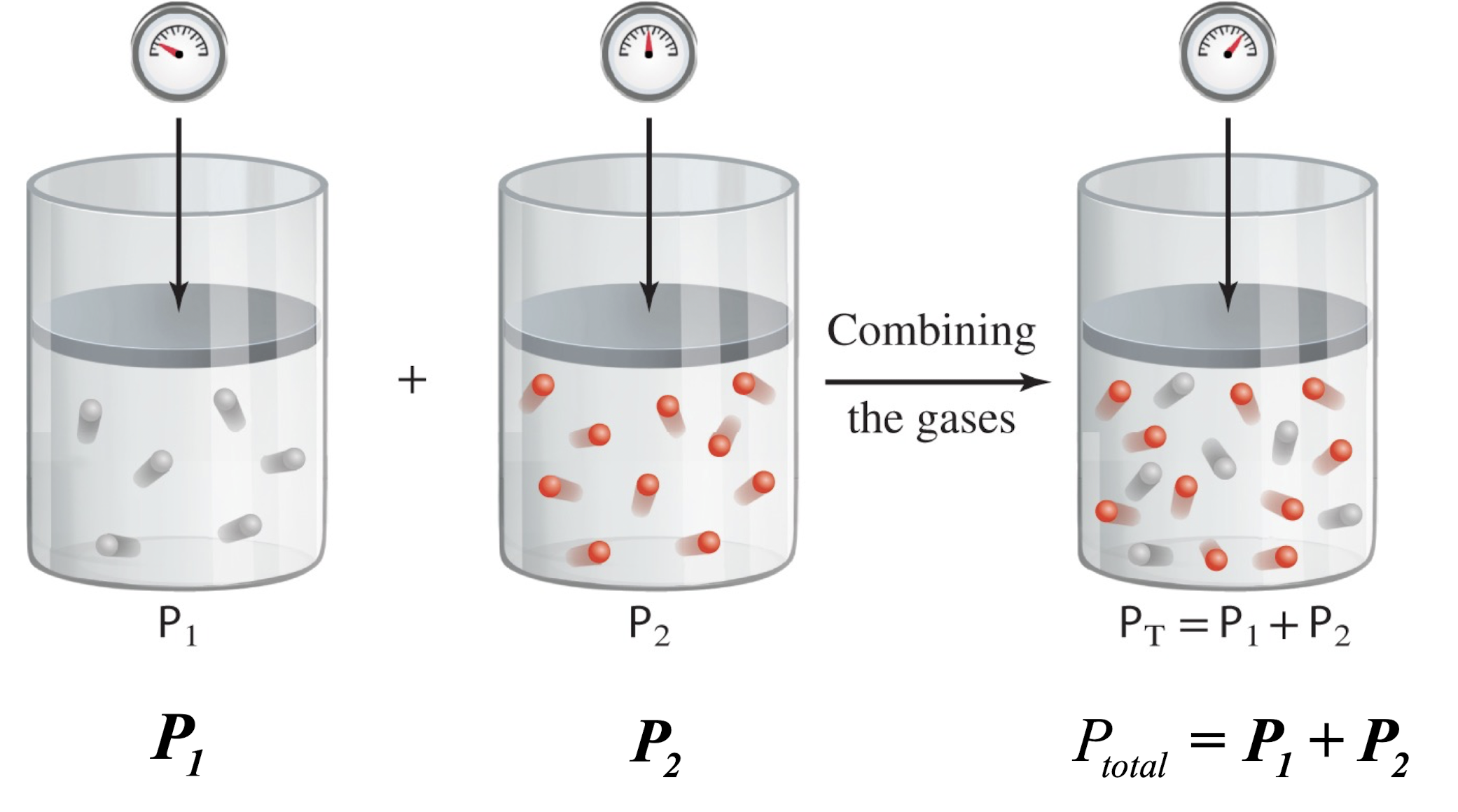
- Volumne과 Temperature가 상수이다. (변하지 않는 값)
- $$P_1 + P_2 = P_{\text{total}}$$
[2] 부분 압력 공식
1) 기본 설정
- 부피 V인 용기에 두 가지 기체 A와 B가 존재
- R: 기체상수
- T: 온도
2-1) 기체 A의 부분압력
$P_A = \frac{n_A RT}{V}$
- $n_A$: A의 몰수
2-2) 기체 B의 부분압력
$P_B = \frac{n_B RT}{V}$
- $n_B$: B의 몰수
2-3) 전체 압력 (달톤의 분압 법칙)
$P_T = P_A + P_B$
3-1) 몰분율 (Mole Fraction)
3-2) 기체 A의 몰분율
$X_A = \frac{n_A}{n_A + n_B}$
3-3) 기체 B의 몰분율
$X_B = \frac{n_B}{n_A + n_B}$
4. 부분압력과 몰분율의 관계
개별 기체
$P_A = X_A P_T$
$P_B = X_B P_T$일반화된 식
$P_i = X_i P_T$
- 여기서 i는 임의의 기체를 나타내며, $X_i$는 다음과 같이 정의 된다.
- $X_i = \frac{n_i}{n_T} = \frac{n_i}{\sum_{i=1}^n n_i}$
[3] 물로 기체 수집하기
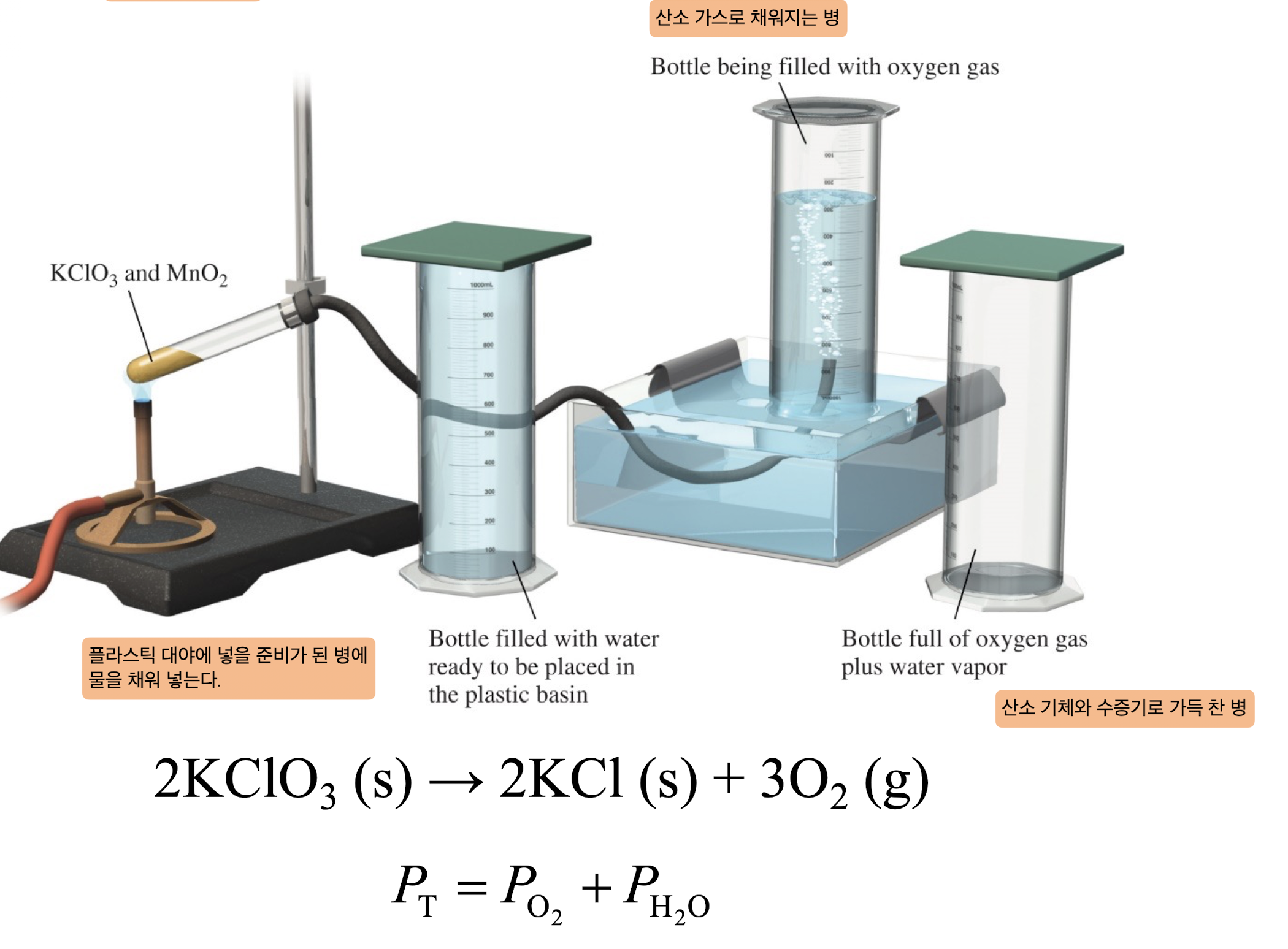
1) 과정
- 플라스틱 대야에 넣을 준비가 된 병에 물을 채워 넣는ㄴ다.
- 산소로 가득 채워지는 병
- 산소 기체와 수증기로 가득 찬 병
-> $P_T = P_{O_2} + P{H_2}O$
2) 기체 수집
: 물을 통해 기체를 수집하는 방법은 반응으로 발생하는 산소와 같은 기체를 쉽게 모을 수 있는 실험이다.
3) 증기압
: 물을 통해 수집할 때 기체에 포함되는 수증기의 압력 ($PH_2O$)을 고려해야 하며, 산소 기체의 실제 압력은 물의 증기압을 제외한 값으로 계산한다.
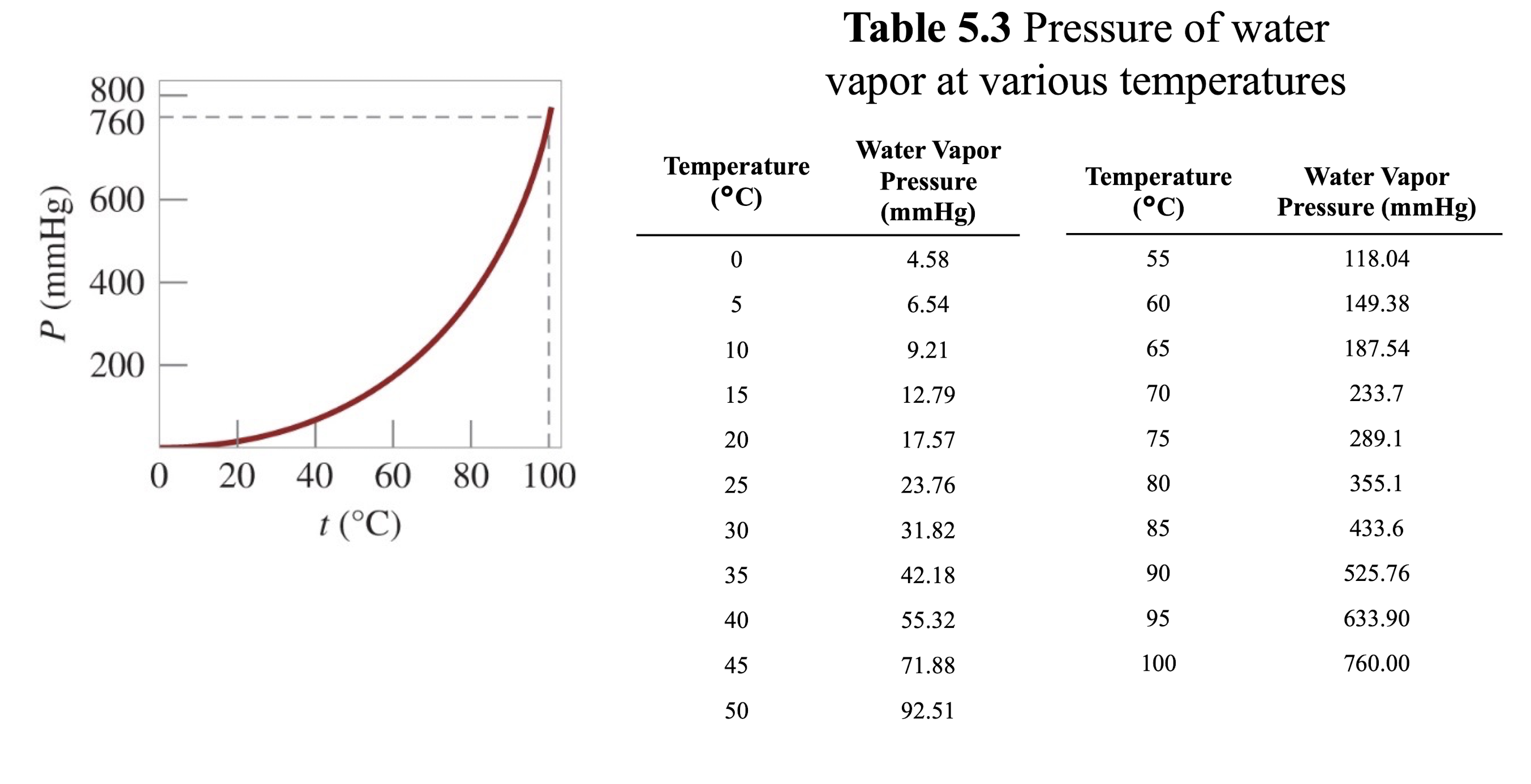
[4] 수증기의 온도
: 다양한 온도에서의 수증기의 압력은 상이하다. (온도가 높아질수록, 압력은 높아진다.)

728x90
'한동대학교 > 일반화학' 카테고리의 다른 글
| [일반화학] Chapter 6 - (2) (0) | 2025.03.16 |
|---|---|
| [일반화학] Chapter 6 - (1) (0) | 2025.03.14 |
| [일반 화학] Chapter 5 - (1) (0) | 2025.03.14 |
| [일반화학] Chapter 4 - (3) (0) | 2025.03.14 |
| [일반화학] Chapter 4 -(2) (0) | 2025.03.14 |




