Notice
Recent Posts
Recent Comments
Link
250x250
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
Tags
- GLS
- 날솟샘
- 예배
- 전산전자공학부
- 고윤민교수님
- FE
- 네트워킹
- csee
- 컴네
- 날마다 솟는 샘물
- 어노인팅
- 한동대학교
- Database
- SQL
- QT
- 데이터베이스
- 묵상
- 유태준교수님
- 프론트엔드
- 일반화학
- 찬양
- 설교
- computer networks and the internet
- dbms
- SQLD
- CCM
- 글로벌리더십학부
- 화학
- CHEMISTRY
- 혼자공부하는sql
Archives
- Today
- Total
멈추지 않는 기록
[일반화학] Chatper7 - (3) 본문
728x90
일자 : 24-2 12주차 2차시
(안함) [7] Chemistry in Action: Laser – The Splendid Light~~
: 행동하는 화학: 레이저 - 찬란한 빛
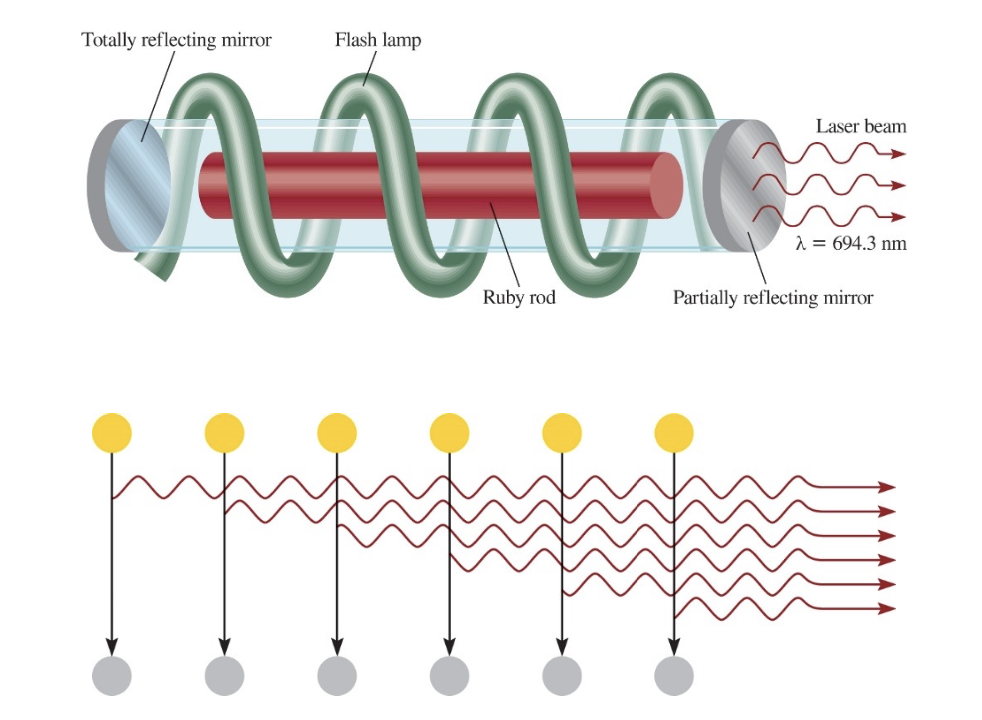
1) 레이저 빛의 주요 특성
- 강렬함 (Intense)
- 단일 에너지 (Monoenergetic)
- 일관성 (Coherent)
7.4 The Dual Nature of the Electron
: 전자의 이중성
[1] 전자 에너지의 양자화
왜 전자의 에너지는 양자화(quantized)되어 있을까?
드브로이 (1924)는 전자가 입자이면서 동시에 파동의 성질을 가지고 있다고 설명했다.
1) 수식
- $2\pi r = nλ$
- λ = $\frac h {mu}$
- u = velocity of $e^-$ (전자의 속도)
- m = mass of $e^-$ (전자의 질량)
(안함) [2] Chemistry in Action: Electron Microscopy
: 화학의 실제 적용: 전자현미경
- $λ_e$ = 0.004 nm
- 동일한 사람에게서 채취한 정상 적혈구와 겸상 적혈구의 전자현미경 사진.
7.5 Quantum Mechanics
: 양자 역학
7.6 Quantum Numbers
: 양자수
[1-1] 슈뢰딩거 파동 방정식 1
- 1926년에 슈뢰딩거는 전자의 입자와 파동 성질을 모두 설명하는 방정식을 작성하였다. 이 방정식에서 사용된 파동 함수 (ψ)는 다음을 설명한다.
- 주어진 (ψ) 값에서 전자의 에너지
- 특정 공간 내에서 전자를 발견할 확률
- 슈뢰딩거 방정식은 수소 원자에 대해서만 정확히 해를 구할 수 있으며, 다전자계에서는 근사적으로 해결해야 한다.
[1-2] 슈뢰딩거 파동 방정식 2
y is a function of four numbers called quantum numbers (n, l, $m_l$, $m_s$)
- n = 1, 2, 3, 4, .…
distance of $e^-$ from the nucleus
[1-2] 슈뢰딩거 파동 방정식 2
- ψ는 양자수 네 개 $n, l, m_l, m_s$로 불리는 숫자들의 함수이다.
- 주양자수 $n$
- $n = 1, 2, 3, 4, \dots$
- 음수는 불가능하다. (오직 양수만 가능)
- 전자의 핵으로부터의 거리
[1-3] 슈뢰딩거 파동 방정식 3
- quantum numbers (양자수) : (n, l, $m_l$, $m_s$)
- angular momentum quantum number l (각운동량 양자수 l)
- for a given value of n, l= 0, 1, 2, 3, ... n-1
- n = 1, l = 0
- n = 2, l = 0 or 1
- n = 3, l = 0, 1 or 2
- 주기율표
- l = 0 -> s orbitall (오르비탈)
- l = 1 -> p orbital (오르비탈)
- l = 2 -> d orbitall (오르비탈)
- l = 3 -> f orbitall (오르비탈)
- 전자가 차지하는 공간의 "형태"
[1-4] 슈뢰딩거 파동 방정식 4
- quantum numbers (양자수) : (n, l, $m_l$, $m_s$)
- magnetic quantum number (자기 양자 수) $m_l$
- for a given value of l
- $m_l$ = -l, ....., 0, ...., + l
- if l = 1 (p orbital), $m_l$ = -1, 0, or +1
- if l = 2 (d orbital), $m_l$ = -2, -1, 0, or + 1
- 우주에서 궤도의 방향
[1-5] 슈뢰딩거 파동 방정식 5
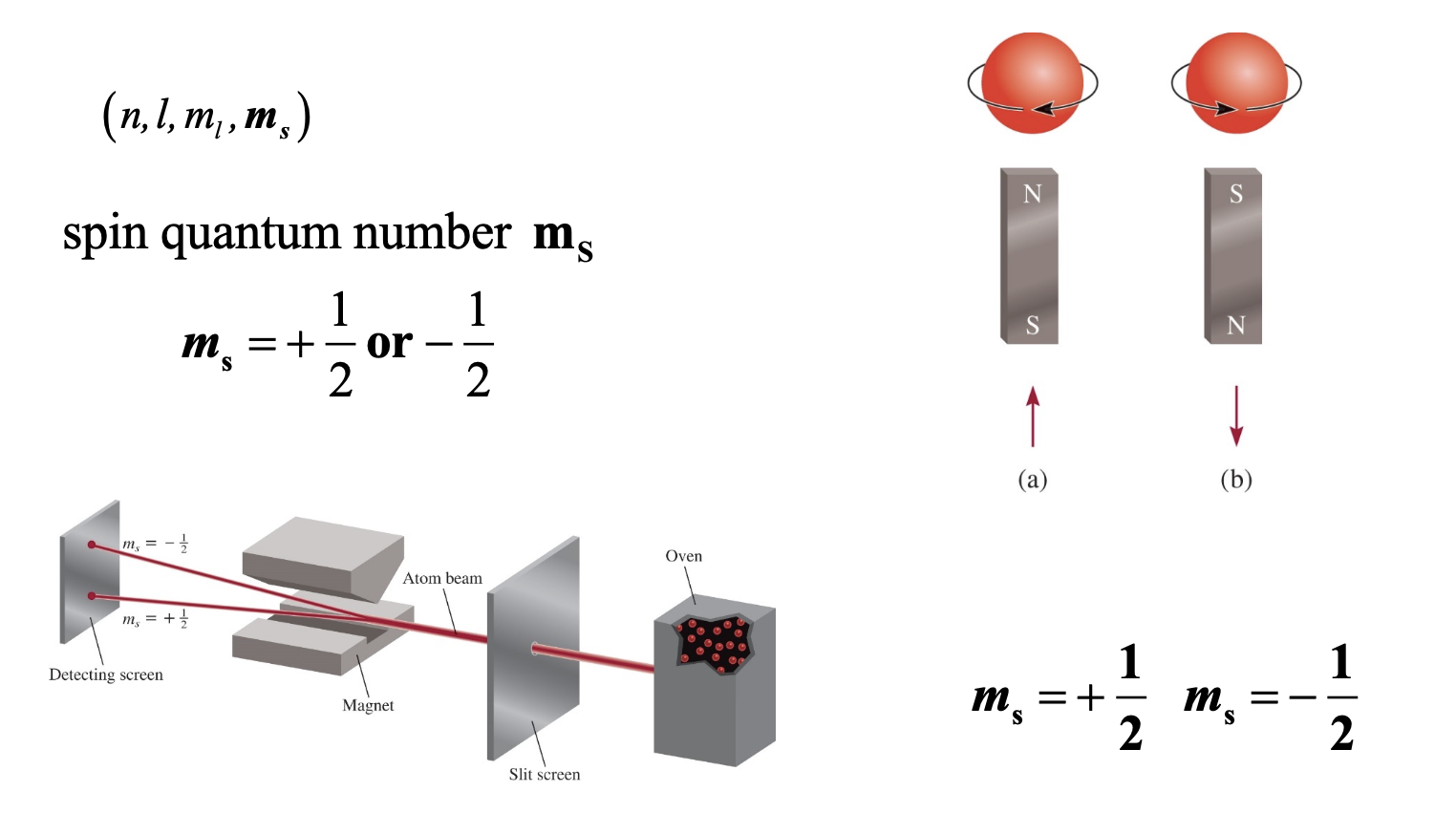
1) 양자수 표기:
- (n, l, ml, ms) 형태로 표시됨
- 스핀 양자수 $m_s$는 +1/2 또는 -1/2 두 가지 값만 가질 수 있음
2) 스핀의 시각적 표현:
- 빨간 구체가 회전하는 방향으로 스핀을 표현
- N극과 S극이 있는 막대자석으로 스핀 방향 표시
- (a)는 위쪽 방향($m_s$ = +1/2)
- (b)는 아래쪽 방향($m_s$ = -1/2)
3) Stern-Gerlach 실험 장치 구성:
- Oven (원자 소스)
- Slit screen (슬릿 스크린)
- Magnet (자석)
- Detecting screen (검출 스크린)
- Atom beam (원자 빔)
4) 실험 결과:
- 원자 빔이 자기장을 통과하면서 두 개의 경로로 분리됨
- 위쪽 경로: $m_s$ = +1/2
- 아래쪽 경로: $m_s$ = -1/2
이 실험은 전자의 스핀이 양자화되어 있다는 것을 증명하는 중요한 실험으로, 원자의 스핀 상태가 연속적이지 않고 이산적인 값을 가진다는 것을 보여줍니다.
Summary
네, 내용을 다음과 같이 정리해드리겠습니다:
[1] 레이저의 특성
- 세 가지 주요 특성: 강렬함(Intense), 단일 에너지(Monoenergetic), 일관성(Coherent)
[2] 전자의 이중성 (7.4)
- 드브로이 (1924): 전자는 입자이면서 동시에 파동의 성질을 가짐
- 주요 수식: $2\pi r = nλ$, λ = $\frac h {mu}$
- u: 전자의 속도
- m: 전자의 질량
[3] 슈뢰딩거 파동 방정식 (7.6)
A. 기본 개념
- 1926년 발표
- 파동 함수(ψ)로 전자의 에너지와 위치 확률 설명
- 4개의 양자수로 구성: (n, l, ml, ms)
B. 양자수 설명
주양자수(n)
- 값: 1, 2, 3, 4, ... (양수만 가능)
- 핵으로부터의 거리 관련
각운동량 양자수(l)
- 값: 0 ~ (n-1)
- 오비탈 종류: s(l=0), p(l=1), d(l=2), f(l=3)
자기 양자수(ml)
- 값: -l ~ +l
- 궤도의 방향 지정
스핀 양자수(ms)
- 값: +1/2 또는 -1/2
- Stern-Gerlach 실험으로 증명
[4] Stern-Gerlach 실험
- 목적: 전자의 스핀 양자화 증명
- 결과: 원자 빔이 두 경로로 분리됨 (ms = +1/2, -1/2)
- 의의: 원자의 스핀 상태가 이산적임을 입증

728x90
'한동대학교 > 일반화학' 카테고리의 다른 글
| [일반 화학] Chapter 7 - (5) (0) | 2025.03.16 |
|---|---|
| [일반화학] Chatper7 - (4) (0) | 2025.03.16 |
| [일반화학] Chapter7 - (2) (0) | 2025.03.16 |
| [일반화학] Chapter7 - (1) (0) | 2025.03.16 |
| [일반화학] Chapter 6 - (3) (0) | 2025.03.16 |





