일자 : 24-2 13주차 1차시
7.7 원자 오비탈
[1] 양자수와 원자 오비탈
1) 정의
양자수 (Quantum Numbers): 양자수는원자 내 전자의 상태를 설명하는 숫자- 전자가
특정 에너지 상태에 있을 때의 위치와 에너지등을 정의한다.
- 전자가
원자 오비탈: 전자가원자핵 주변에서 발견될 확률이 높은 공간- 각 오비탈은
고유한 모양과 에너지를 가지고 있으며,양자수에 의해 정의된다.
- 각 오비탈은
2) 양자수와 원자 오비탈의 관계
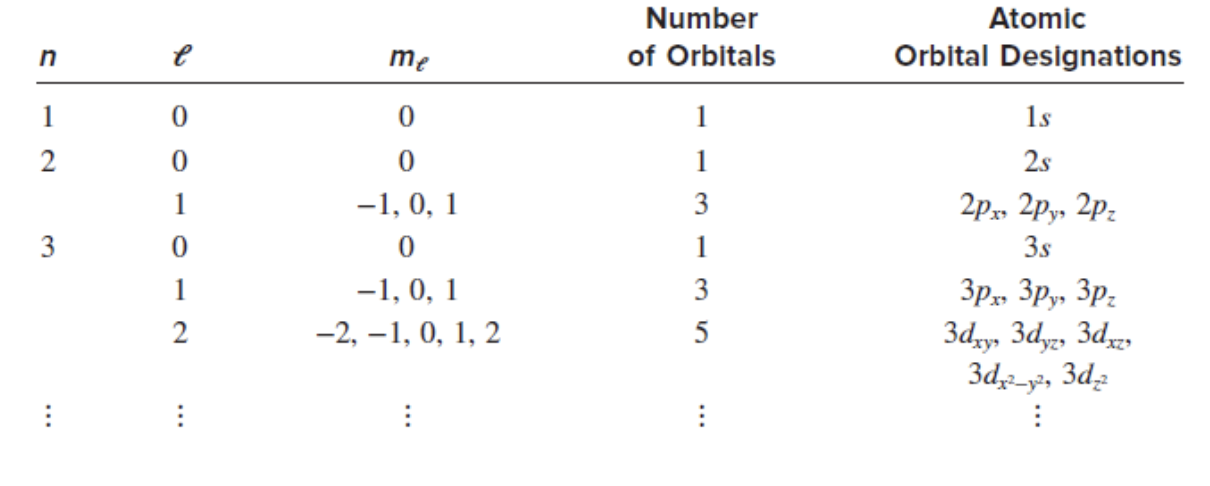
- n (주양자수, Principal Quantum Number)
- 전자의 에너지 수준과
전자껍질(shell)을 나타냄. - 값: 양의 정수 $n = 1, 2, 3, \dots$.
- $n$이 클수록 전자의 에너지가 높아지고 원자핵에서 멀어짐.
- 전자의 에너지 수준과
- $e$ (부양자수, Azimuthal Quantum Number, $l$)
오비탈의 모양을 결정.- 값: $l = 0$부터 $n-1$까지의 정수.
- 오비탈 종류:
- $l = 0$: s 오비탈 (구형)
- $l = 1$: p 오비탈 (아령형)
- $l = 2$: d 오비탈
- $l = 3$: f 오비탈
- $m_e$ (자기양자수, Magnetic Quantum Number)
오비탈의 공간적 방향을 나타냄.- 값: $-l$에서 $+l$까지의 정수.
- 예: $l = 1$이면, $m_e = -1, 0, +1$.
- Number of Orbitals
- 각 주양자수 $n$에 대해 존재하는
오비탈의 총 개수. - 공식: $n^2$.
- 예: $n = 2$일 때, 오비탈 개수는 $2^2 = 4$.
- 각 주양자수 $n$에 대해 존재하는
- Atomic Orbital Designations
오비탈의 이름을 양자수에 따라 지정.- 예:
- $n = 1, l = 0$: 1s
- $n = 2, l = 0$: 2s
- $n = 2, l = 1$: 2p
- $n = 3, l = 2$: 3d
[2] 확률 밀도
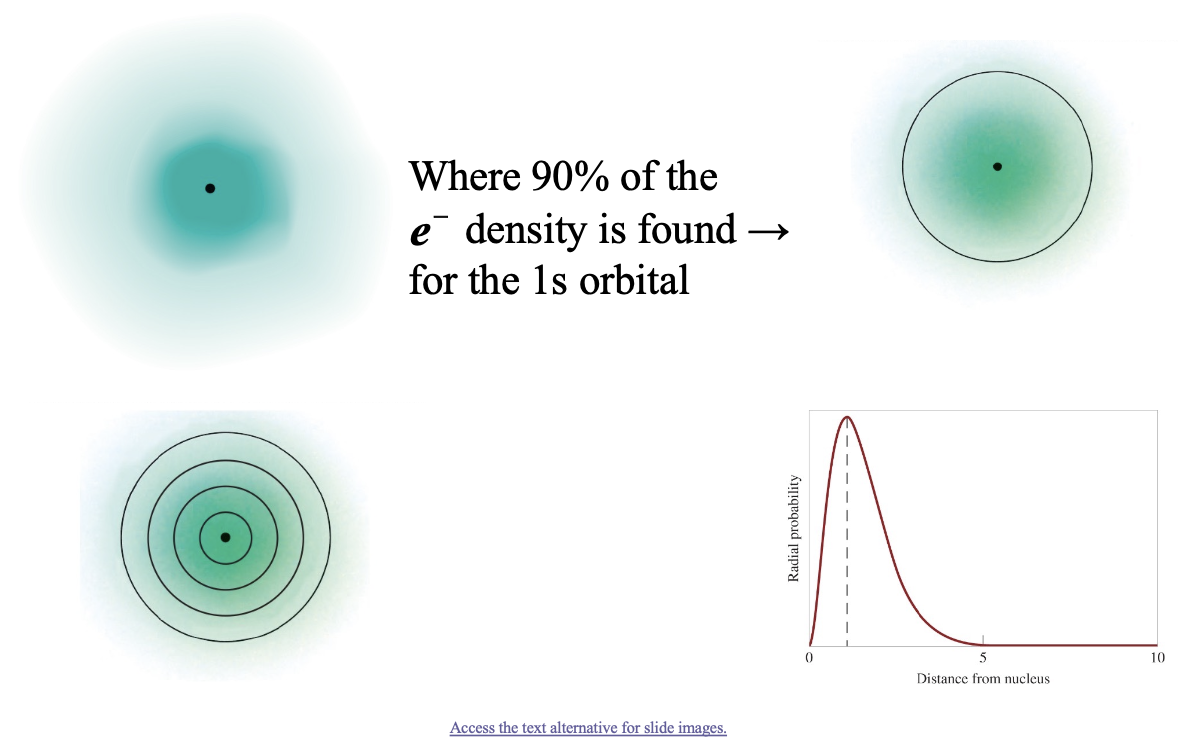
- 전자 밀도의 90%가 발견되는 영역
1s 오비탈의 경우
1) 정의
- 확률 밀도의 정의
- 확률 밀도는
전자가 특정 위치에 있을 가능성을 나타내는 양이다. - 슈뢰딩거 방정식의 해를 통해 얻은 파동 함수 $\psi$의 제곱 $|\psi|^2$이 확률 밀도를 나타낸다.
- 확률 밀도는
- 전자 밀도와 90% 영역
- 원자 오비탈 내에서 전자의 위치를 정확히 특정할 수 없으므로, 전자가 발견될 확률이 90% 이상인 영역을 정의한다.
- 이 90% 확률 영역은 원자 오비탈의 경계를 시각적으로 나타낸다.
[3] 원자 오비탈
1) $l = 0$ (s 오비탈)
- $l$ 값이 0일 때, 원자 오비탈은 구형 대칭을 가지며 이를 s 오비탈이라 부른다.
- s 오비탈은 모든 방향에서 대칭적인 구조로, 원자핵을 중심으로 전자 구름이 퍼져 있는 형태이다.
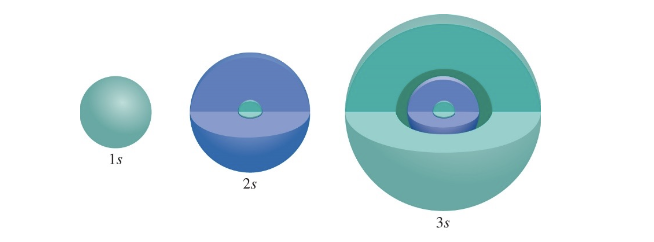
설명:
s 오비탈은 가장 단순한 형태로, $1s$, $2s$, $3s$와 같이 주양자수($n$)에 따라 크기만 달라지며 구형 대칭을 유지한다. 이는 원자핵에 가까운 영역에서 전자 밀도가 가장 높고, 핵에서 멀어질수록 밀도가 감소한다.
2) $l = 1$ (p 오비탈)
- $l$ 값이 1일 때, p 오비탈이라 하며, 두 개의 뚜렷한 "엽(lobe)"을 가진 형태로 나타난다.
- p 오비탈은 $x$, $y$, $z$ 축을 기준으로 3가지 방향성($p_x$, $p_y$, $p_z$)을 가진다.
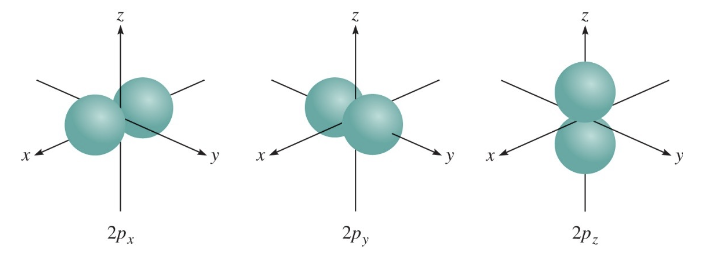
설명:
p 오비탈의 구조는 특정 축을 중심으로 대칭적이며, 전자는 두 엽에 걸쳐 분포한다. 이로 인해 원자 내 화학 결합 시 방향성이 중요한 역할을 하며, 분자의 형태와 결합각에 영향을 준다.
3) $l = 2$ (d 오비탈)
- $l$ 값이 2일 때는 d 오비탈이라 하며, 더 복잡한 구조를 가진다.
- 4개의 엽이 있는 "클로버" 모양과 고리 구조를 포함한 다양한 형태가 있으며, 공간에서 5가지 방향성을 가진다.
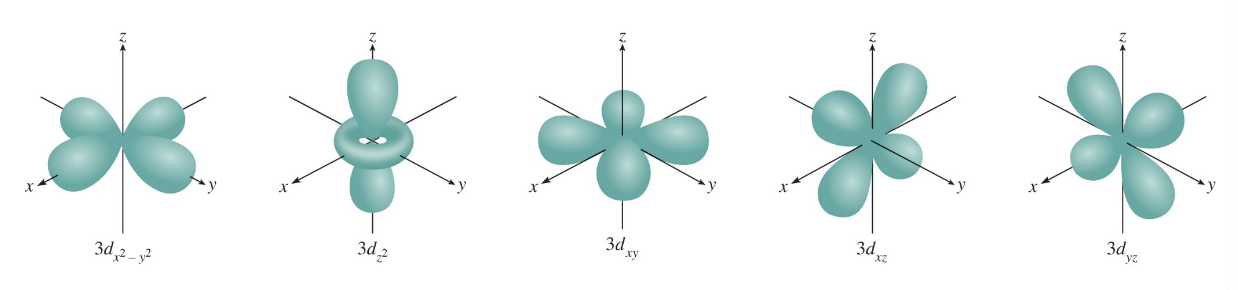
설명:
d 오비탈은 화학적으로 다전자 원자의 전자 배열에서 중요한 역할을 한다. 특히, 전이 금속 원소의 특성(예: 착화합물의 색과 자기적 성질)은 d 오비탈의 전자 배치에 크게 영향을 받는다.
[4] 오비탈의 방향성
1) $m_l = -1, 0, 1$
- 자기 양자수($m_l$)가 $-1$, $0$, $1$일 경우, 오비탈은 3가지 방향을 가진다.
- 이는 주로 p 오비탈에 해당하며, $p_x$, $p_y$, $p_z$와 같이 공간에서의 특정 방향으로 정의된다.
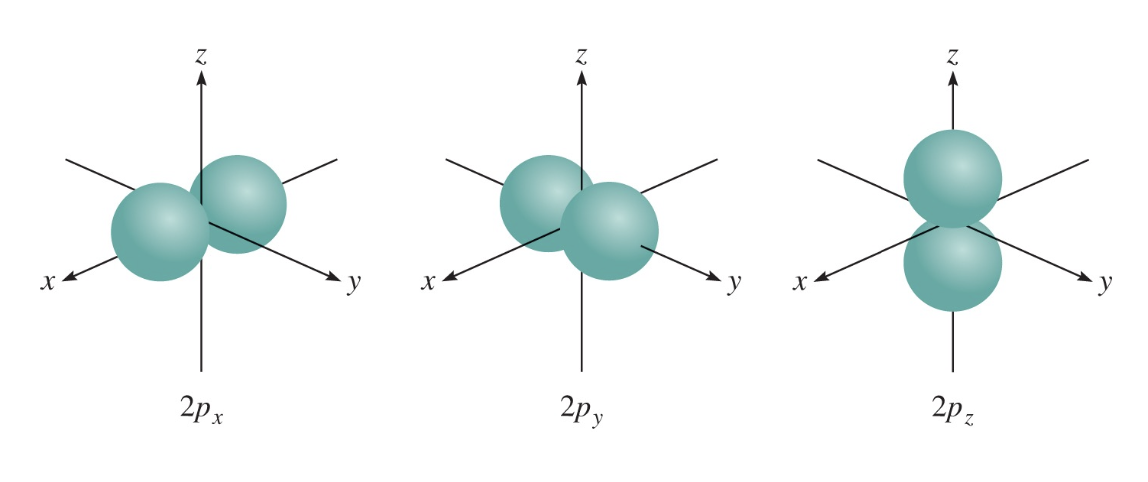
설명:
p 오비탈의 방향성은 원자가 결합 시 분자의 기하학적 구조에 영향을 미친다. 예를 들어, 탄소 원자의 4개의 p 오비탈이 혼성화될 경우 사면체 구조를 형성하여 화학적 안정성을 제공한다.
2) $m_l = -2, -1, 0, 1, 2$
- 자기 양자수($m_l$)가 $-2$, $-1$, $0$, $1$, $2$일 경우, 오비탈은 5가지 방향을 가진다.
- 이는 d 오비탈에 해당하며, 공간에서의 다양한 대칭 구조와 방향성을 나타낸다.
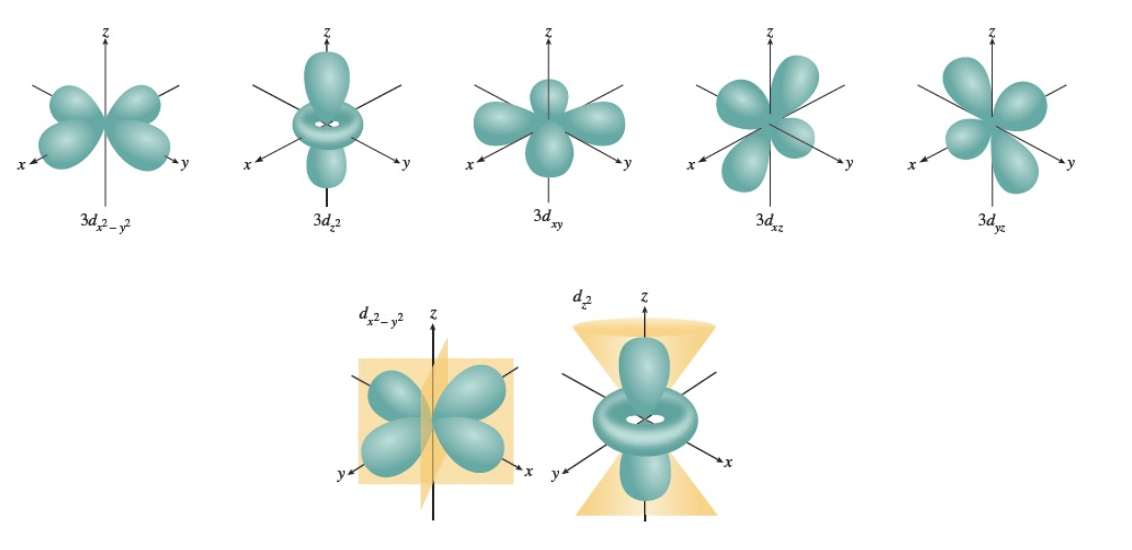
설명:
d 오비탈의 방향성은 전이 금속과 리간드 사이의 결합에서 중요한 역할을 한다. 리간드의 전자 구름이 특정 방향의 d 오비탈과 상호작용하여 결합이 형성되며, 이러한 상호작용은 착화합물의 색, 자기적 특성, 촉매 작용 등에 기여한다.
[5] 슈뢰딩거 파동 함수
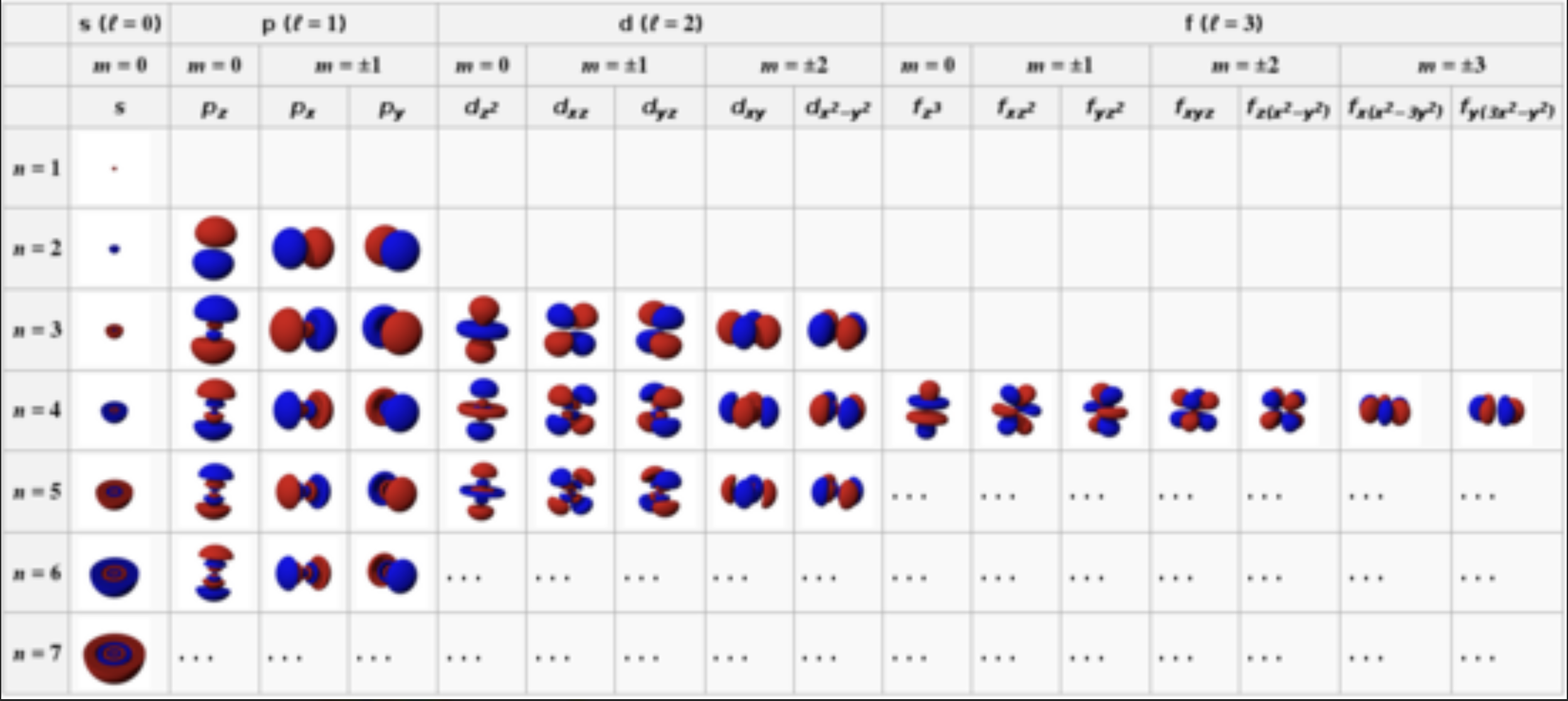
1) 양자수: ($n, l, m_l, m_s$)
- 전자가 원자 내에서 존재하고 그 에너지를 가지는 방식은 고유한 파동 함수(ψ)로 기술된다.
- 파울리 배타 원리에 따르면, 한 원자 내에서 두 전자가 동일한 네 가지 양자수를 가질 수 없다.
(이 원리가 없다면 물질은 존재할 수 없다!)
2) 껍질, 부껍질, 오비탈
- 껍질(shell): 같은 주양자수($n$)를 가지는 전자들의 집합.
- 부껍질(subshell): 같은 주양자수($n$)와 각운동량 양자수($l$)를 가지는 전자들의 집합.
- 오비탈(orbital): 같은 $n$, $l$, $m_l$ 값을 가지는 전자들.
설명:
파동 함수는 전자의 위치 확률 밀도를 기술하며, 양자수는 전자의 에너지 상태와 공간 분포를 정의하는 데 사용된다. 파울리 배타 원리는 전자 배치 규칙과 화학적 안정성의 근본적인 기초가 된다.
[6-1] 단전자 원자에서의 오비탈 에너지
1) 에너지는 주양자수($n$)에만 의존한다.
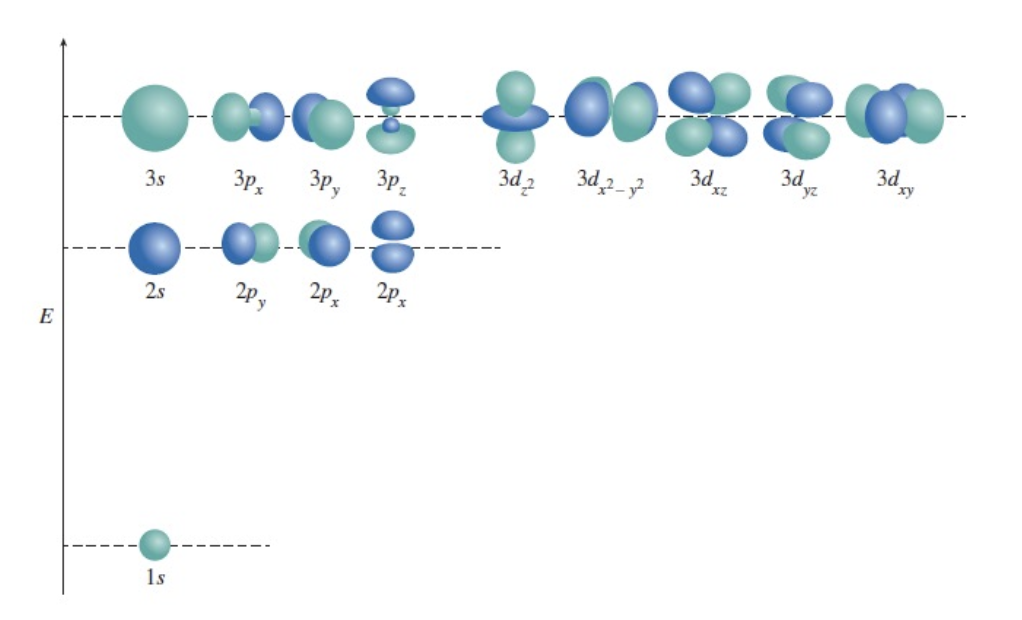
설명:
수소 원자처럼 단전자 시스템에서는 오비탈의 에너지가 $n$ 값에만 의존하며, $l$ 값의 차이는 없다. 따라서 $2s$와 $2p$의 에너지는 동일하다.
[6-2] 다전자 원자에서의 오비탈 에너지
1) 에너지는 $n$과 $l$에 의존한다.
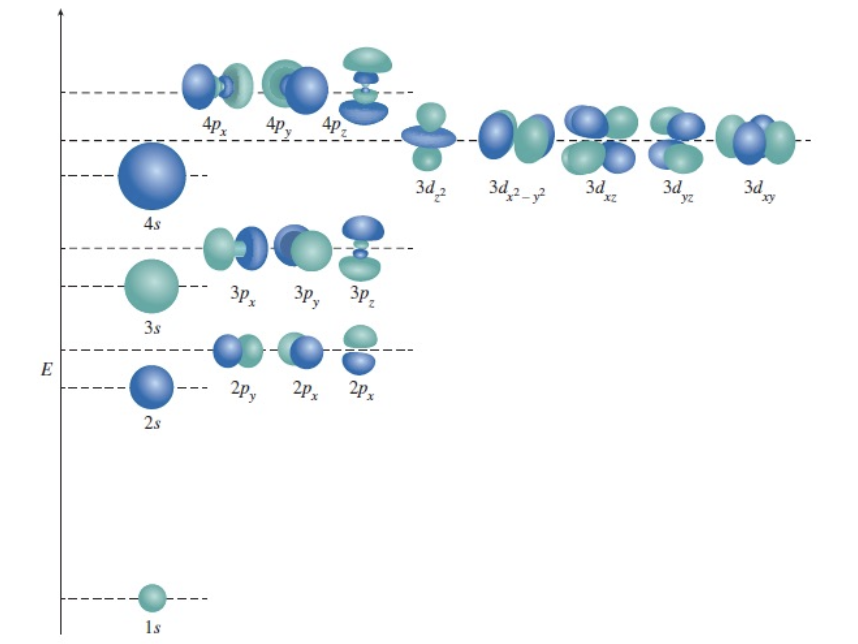
설명:
다전자 원자에서는 전자 간 반발로 인해 같은 $n$ 값을 가지더라도 $l$ 값에 따라 에너지가 달라진다. $s$ 오비탈의 에너지는 $p$, $d$, $f$ 오비탈보다 낮으며, 이는 전자 배치와 화학적 성질에 영향을 준다.
[7] Aufbau 원리
- 전자는 에너지가 낮은 오비탈부터 차례로 채워진다.
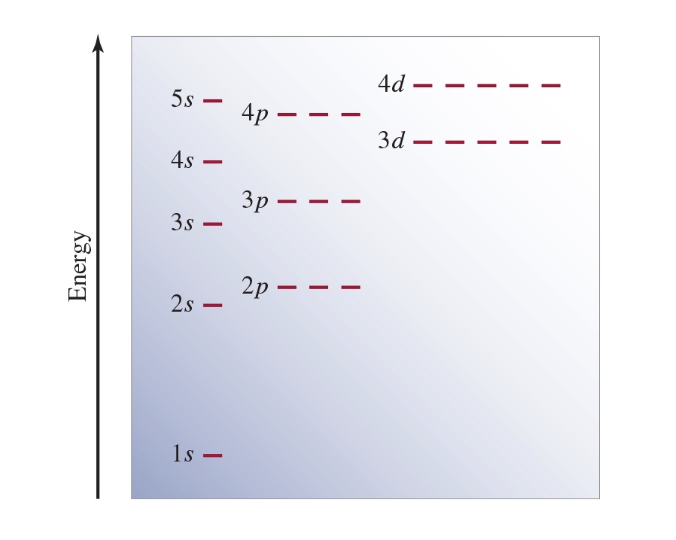
설명:
Aufbau 원리는 전자 배치의 기본 원칙으로, 화학 원소의 주기적 성질을 설명하는 데 중요한 역할을 한다. 낮은 에너지를 선호하는 경향은 원자의 안정성을 높인다.
[8] 훈트의 규칙
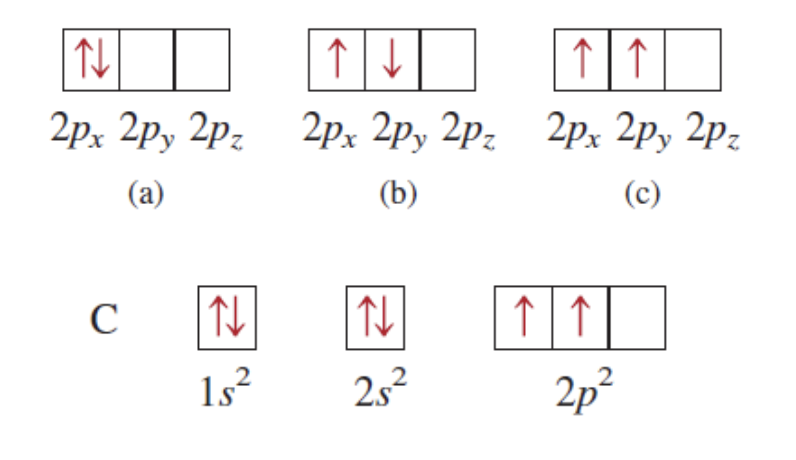
- 가장 안정한 전자 배치는 같은 부껍질 내에서 가능한 한 많은 전자들이 평행 스핀을 가지는 경우이다.
설명:
훈트의 규칙은 전자 간의 반발을 최소화하여 원자의 에너지를 낮춘다. 예를 들어, $p$ 오비탈에서 세 전자가 각각 다른 오비탈($p_x$, $p_y$, $p_z$)에 배치되며 동일한 스핀을 가지는 경우 에너지가 가장 낮다.
[9] 다전자 원자의 오비탈 채움 순서
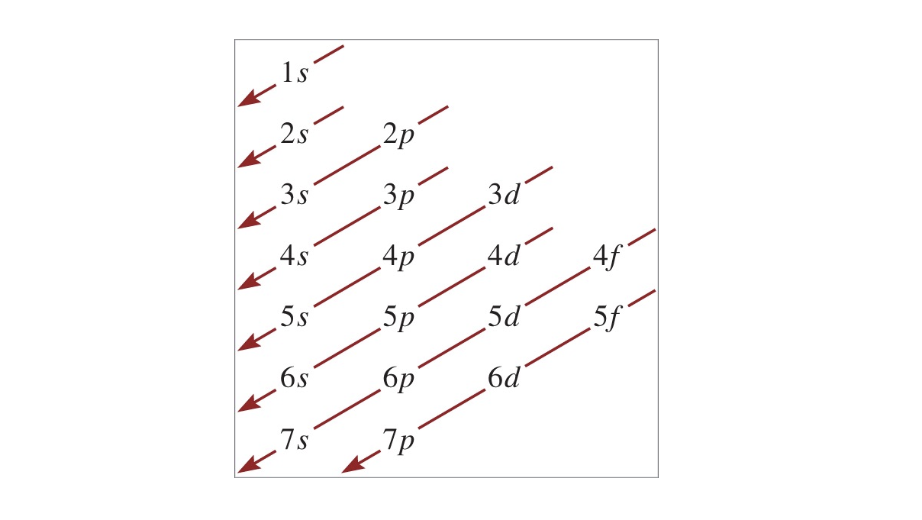
- $1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s$
설명:
오비탈의 채움 순서는 에너지 수준에 따라 결정되며, 이는 주기율표의 구조와 원소의 화학적 성질을 이해하는 데 필수적이다. $4s$ 오비탈이 $3d$보다 먼저 채워지는 것은 전자의 상호작용과 에너지 최적화의 결과이다.

'🏫 한동대학교 > 일반화학' 카테고리의 다른 글
| [일반 화학] Chapter 8 - (1) (0) | 2025.03.16 |
|---|---|
| [일반 화학] Chapter 7 - (5) (0) | 2025.03.16 |
| [일반화학] Chatper7 - (3) (0) | 2025.03.16 |
| [일반화학] Chapter7 - (2) (0) | 2025.03.16 |
| [일반화학] Chapter7 - (1) (0) | 2025.03.16 |
